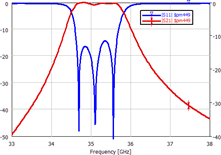
S-Parameters Extraction
Area of applications of QuickWave software for electromagnetic design and simulations.
S-Parameters extraction, including Sk1 parameters for reciprocal circuits and full S-matrix calculations, S-Parameters extraction below cutoff frequency, frequency dependent wave impedance, propagation constant, standing wave ratio and group delay, power balance calculations, S-Parameters extraction for virtually shifted reference (calculation) plane, etc.